“关于三角形的一些概念”教学设计

[教学目标]

1．会说出怎样的图形叫三角形，并会用符号语言表示一个三角形。

2．会正确画出锐角三角形所有的角平分线、中线、高，并会用符号语言表述某一条线段是三角形的角平分线、中线和高。

此外，从多个角度观察图形的活动中，逐步培养学生灵活、发散的思维习惯。

[引导性材料]

生活中我们看到许许多多的三角形，比如少先队员佩带的红领巾、自行车的三角支架、空调外机的支架等，三角形是一种简单又常见的图形，小学数学中我们学习了有关三角形的一些初步知识，现在你能阐述怎样的几何图形叫三角形吗?

[教学设计]

问题1：以下是三位同学描述三角形的三种不同的说法，你认为其中恰当的说法是哪种?

（1）由三个角组成的图形叫三角形；

（2）由三条线段组成的图形叫三角形；

（3）由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫三角形。

问题2：你能说明问题1中（l）、（2）两种说法不恰当吗?

说明和建议：几何概念是对一类对象共同的本质属性的规定教学中通常较多采用教师主动给出的方法，这里设计问题1的实质是创设让各类学生主动参与概念教学活动的情景，并通过问题2的探究（教学中学生通常都能画反例来说明），有利于学生会运用举反例来说明某个命题是假命题的简捷的说理方法同时便于学生对三角形的感性认识上升到本质的抽象。

学生阅读课本第2页第1～4段（三角形的边、三角形的顶点、三角形的角的概念以及它们的表示方法）。

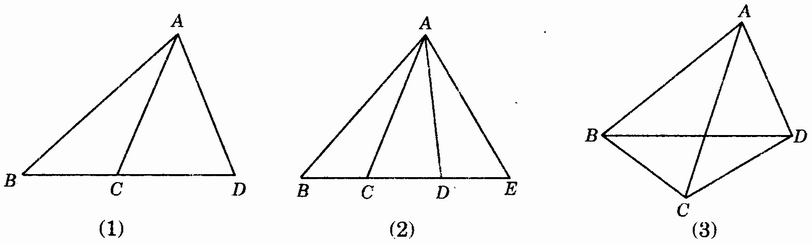
图3．1－1

练一练：在上面一组图形（图3．1－1）中：

（1）分别有几个三角形?说出这些三角形；

（2）说出各个图形中以点B为顶点的角所对的边。

说明和建议：1．这是一组由简单到复杂的识图训练题。图（1）中有3个三角形，图（2）中有6个三角形，图（3）中有8个三角形。

2．设计这一组识图题的实质是帮助学生进行图形的分解，从而正确认识图形。所谓“图形的分解”就是从复杂的图形中分解出若干个简单图形。比如图3．l－1（2）可以分解为图形（1）那样的两个简单图形，图形（3）可以分解为图形（1）那样的简单图形四个。

3．在教学中，还可以帮助学生多角度观察图形。比如图3．1－l（2）中的所有的三角形有公共顶点A，并且都有一条边在线段BE上，因此这个图形还可以分解成（如图3．1－2）表示线段和差、角的和差的图形。

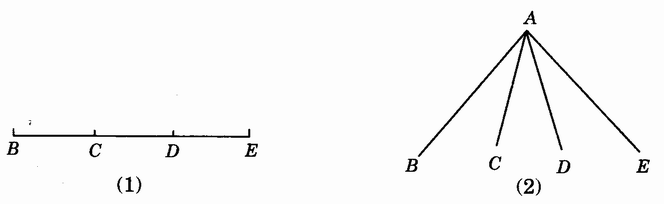
图3．1－2

图3．l－2（1）中，有四个点六条线段。所以分别以这6条线段为边的三角形有6个；图3．1－2(2)中，有四条射线六个角，同样地，分别以这6个角为内角的三角形有6个。图3．1－2是学生早已熟悉的简单图形，帮助学生从熟悉的简单图形基础上认识新的复杂图形，有利于学习建立新旧知识的联系，同时也为后续的“全等三角形判定”的论证教学中，使学生能主动寻求不同的思路问题和解决问题的途径创造有效的前提。

观察和思考：图3．1－3中，用一根红色的橡皮筋的一端固定在△ABC的顶点A。再把橡皮筋的另一端从点B沿着BC边移动到点C观察移动过程中形成的无数条线段（AD、AE、AF、AG…）中，有没有特殊位置的线段?你认为有哪些特殊位置?

说明：设计让学生在固定的背景（△ABC）中观察橡皮筋在运动情景中形成的多种不同位置的线段，由于前面已学习了角平分线、线段中点、垂线、因此学生很容易发现在固定的背景中运动着的对象中的特殊对象──三角形的角平分线、中线和高，并对它们都有长度这个本质特征也有了新的感知，为正确理解三角形的重要线段的定义奠定了基础。

操作：用纸任意剪三个锐角三角形。按下列要求用折纸的方法折出线段：

（1）三角形的所有的角平分线；

（2）三角形的所有的中线；

（3）三角形的所有的高。

说明和建议：1．折纸活动中有少数学生折三角形的中线和高有错误或困难，教学中教师作示范并及时纠错。

2．三角形的三种重要线段都是用连结顶点──对边(或对边所在直线)

上一个特殊点的方法来定义的，所以具体折纸的过程(先确定折痕的两个端点，再确定折痕)，为学生具体形象地叙述它们的定义增加了清晰的感性认识。

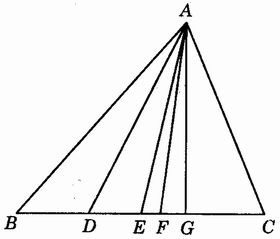
图3．1－3

问题3：请你借助折纸的方法来描述三角形的中线、三角形的角平分线、三角形的高。

问题4：从折纸中你发现锐角三角形有几条角平分线?几条中线?几条高?你还能得到什么结论?

看图（图3．l－3）填空：

（1）∵AE是的△ABC角平分线，

∴∠____=∠____=1/2∠____()。

（2）∵AF△ABC的中线，

∴∠____=∠____=1/2∠____()。

（3）∵AG△ABC的高，

∴∠____=∠____=90°()。

[例题解析]

例：如图3．1－4，∠ACE=∠BCE，BD=CD，指出图中三角形的特殊线段。

解：CE是△ABC的角平分线，

AD是△ABC的中线，

ED是△EBC的中线，

CF是△ACD的角平分线。

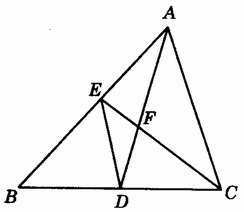
图3．1－4

［小结]

1．学习三角形的有关概念，不仅要弄清它们的意义，而且要学会在复杂的图形中，从不同的角度认识同一个角（或边）的不同的“身份”。

2．三角形的角平分线、中线、高都是线段。三角形的角平分线、高与角的平分线、垂线既有联系也有区别，前者是线段，后者是射线和直线。

3．三角形的三条角平分线交于一点，三条中线交于一点，三条高交于一点。

［作业］

课本习题3．1A组第二题。