“角的比较”教学设计

[教学目标]

1．会用两种方法比较两个角的大小，会用量角器画一个角等于已知角。

2．知道两角的和、差、几倍和几分之一的意义，能说出和写出角的和、差、几倍和几分之一。

3．能说出角平分线的定义，并能用符号语言表示。

此外，培养学生认识几何图形的能力和用几何语句说明道理的能力。

［引导性材料］

上节课研究了角的定义，角的表示方法，对角的概念有了一个比较清楚的认识。角和线段一样是最简单的几何图形，它们有很多类似之处，因此我们可以对照研究。比如，你会用类似于比较线段大小的方法，比较两个角的大小吗?

（让学生回忆并说出两条线段大小比较的两种方法，巩固旧知，并为角的大小比较作铺垫，便于学生进行类比。在学生回答后教师可画出三种比较大小的结果，如图1．5－1。）

图1．5－1

[知识产生和发展过程的教学设计]

1．从比较两线段大小的方法中，能启发你想出比较两个角的大小的方法吗?如图1．5－2，已知∠ABC和∠DEF，如何比较这两个角的大小?

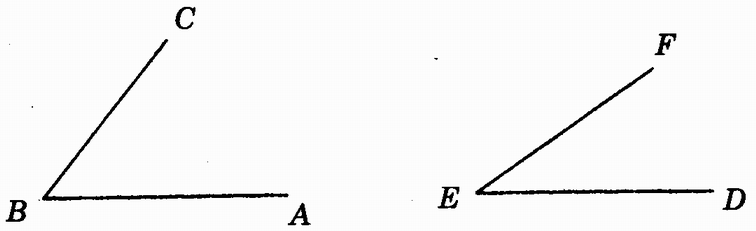
图1．5－2

（让学生四人一小组进行讨论，发表自己的见解，也可以让想不到的方法的学生看了课本第28页所说的方法来复述。教师应制作一个可以任意改变大小的角的模型，让学生到讲台前在黑板上边演示边说明比较方法，并得出三种结论。在黑板上画出如图1．5－3顶点必须重合；一边必须重合；另一边落在其余一边的同旁。角的大小只与角的开口程度有关，而与角的边画出部分的长短无关。）

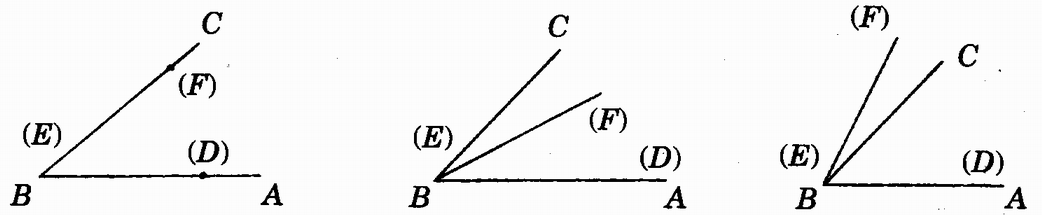
图1．5－3

∠ABC＝∠DEF∠ABC>∠DEF∠ABC<∠DEF

这是通过搬动图形，使它们送合的方法，来比较两个角的大小。

2．请你任意画两个角，用量角器分别量出这两个角的度数，再比较这两个角的大小。

（先画角，再帮助学生回忆用量角器量角的度数的方法，并及时纠正学生使用量角器时出现的错误。提醒学生按下面的步骤操作：（1）对中：顶点对顶点；（2）重合：一边与量角器刻度上的零线重合；（3）读数：读出另一边所在的射线在量角器上的读数。应当告诉学生：用量角器量一个角，一就是看这个角与量角器上哪一个度数的角相等，因此量出了角的度数，就可以按度数来比较它们的大小了。角的大小和它们的度数的大小是一致的。学生这一操作实践，是比较角的大小的又一个方法，即通过“数量”来比较角的大小。）

任意画一个角∠A°B，用量角器画一个角∠COD，使∠COD＝∠AOB，试一试。

（让学生进一步熟悉用量角器量角的度数的方法。并且根据所量得的度数再画一个角使它等于这个度数，也就是等于已知角。这样使学生知道用量角器可以把一个已知角移动到需要的地方去。并掌握用量角器量角和画角的技能。）

3．如图1．5－4(1)、（2）中，分别说出图中∠ABC、∠DEF和∠1、∠2的关系。

（教师先用硬板纸制作上∠1和∠2的模型，按图1．5－－4（1）、（2）所示演示，先放置∠1，再在∠1的外部和内部放置∠2，然后移去纸板，在黑板上画下图1．5－－4(1),让学生观察∠1和∠2的位置特征：图（1）中∠2在∠1的外部，此时有∠ABC＝∠1＋∠2，图（2）中∠2在∠1的内部，此时有∠DEF＝∠1－∠2，还可以从图（1）中得出∠1=∠ABC－∠2，从图（2）中得出∠1=∠DEF＋∠2。让学生从图形中领悟角的和、差的意义。）

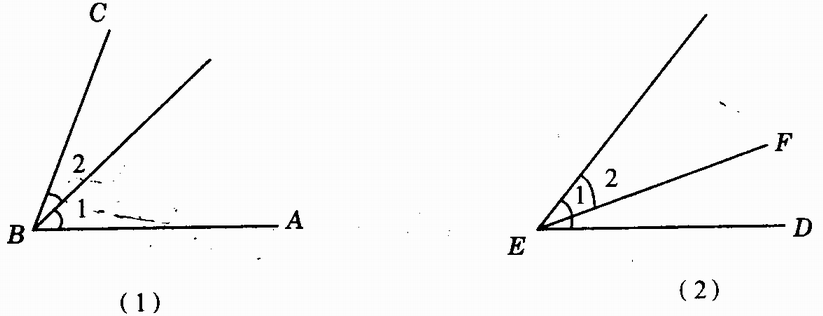
图1．5－4

4．任意画∠1。用量角器画∠AOB=∠1＋∠1。

再画∠COD=∠1＋∠1＋∠1。

图1．5－5

（学生画出如图1．5一5，并在此基础上得出：∠AOB=2∠1，，∠COD=3∠1，∠COD=3∠COE=3∠EOF，，等等，让学生在图形的认识过程中理解角的几倍、几分之一的意义，同时可得出一个角的二等分线有一条，三等分线有2条，n等分线有（n－l）条。）

5．观察图1．5－5（2），射线°C的位置有什么特征?

（通过观察OC是∠AOC和∠BOC的一条公共边，且∠AOC=∠BOC，与线段中点的位置类似，从而让学生说出角平分线的意义，并给出如方框中的符号语言。）

试问：你会用量角器画一个已知角的平分线吗?会画三等分线吗?你能把一个角n等分吗?

(用量角器量出角的度数，再通过计算，把一个角二等分，三等分，．．．n等分，然后画出角的平分线，三等分线．．．，这样让学生感悟数和形的关系。)

[例题解析]

例1图1．5－6中，已知OB是∠AOC的平分线，OD是∠COE的平分线，如果∠AOE=130°，那么∠BOD是多少度?

（本例根据课本第32页习题1．3A组第6题改编而成。通过本例的解答，应用了角平分线的定义、角的和、倍的概念。解题中，要训练学生认识复杂图形的技能，特别是从复杂图形中找出基本图形时，要会排除“干扰”。如说出∠AOE＝∠AOC＋∠COE就应对两条角平分线OB、OD视而不见，求解本例时，要尽可能让学生自己分析、表述。）

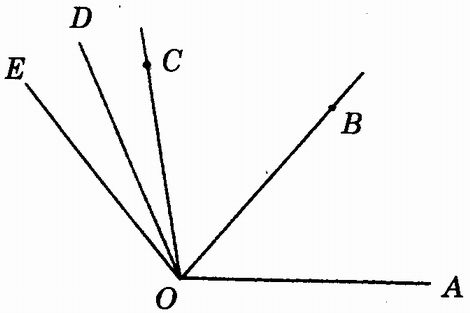
图1．5－6

例2图1．5－－7中，∠1=∠2，试判断∠BAC和∠DAF的大小，并说明理由。

（让学生观察图形，大胆进行猜想，再用简单的几何推理来说明猜想结论的正确。这样，可为后续的推理教学作铺垫。然后教师可演示∠DAE是由∠BAC绕点A旋转而成的，不论旋转到哪一位置，∠BAC与∠DAE总是相等的，以帮助学生从运动的观点来理解角的和、差的概念。）

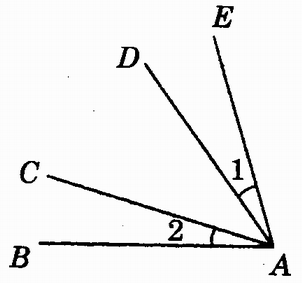
图1．5－7

〔课堂练习〕

1．课本第30页练习第1(口答)、2、3题。

2．如图∠AOC=∠COD=∠BOD，则∠BOC的平分线是_____，∠AOD的平分线是____，3∠COD=_____，=_____=_____，∠AOB的三等分线是_____。

3．图中，OC是∠DOE和∠AOB的平分线。

4．分别说出图中点A、p、Q与∠AOB位置关系。

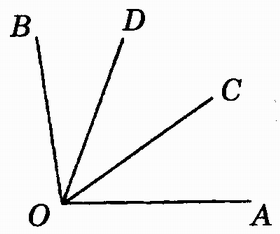
(第2题)

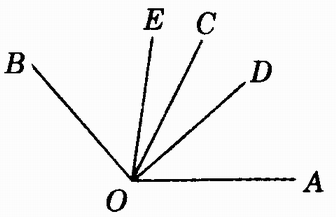
(第3题)

∵OC平分∠AOB，

∴∠AOC=____()。

∵OC平分∠DOE，

∴_____=_____()。

∴∠AOC－∠DOC=∠COB－∠COE(等式性质)，即_____=_____。

［小结］

本节课主要研究了角的大小比较的方法，角的和、差、倍、分的意义和角的平分线的定义、符号语言的表示等内容。可列成下表：

［作业］

1．课本第32页习题1．3A组第3、4、6题，B组第1题。

2．学有余力的学生做B组第2题。