二次根式的化简教学示例 人教课标七年级下册
一、教学目标
1.掌握二次根式的性质
![]()
2.能够利用二次根式的性质化简二次根式
3.通过本节的学习渗透分类讨论的数学思想和方法
二、教学设计
对比、归纳、总结
三、重点和难点
1.重点:理解并掌握二次根式的性质
![]()
2.难点:理解式子![]() 中的
中的![]() 可以取任意实数,并能根据字母的取值范围正确地化简有关的二次根式.
可以取任意实数,并能根据字母的取值范围正确地化简有关的二次根式.
四、课时安排
1课时
五、教具学具准备
投影仪、胶片、多媒体
六、师生互动活动设计
复习对比,归纳整理,应用提高,以学生活动为主
七、教学步骤
(一)教学过程
【复习引入】
1.求值![]() 、
、![]() 、
、![]() 、
、![]() …
…
求值![]() 、
、![]() 、
、![]() 、
、![]() …
…
结论:当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
2.求值![]() 、
、![]() …
…
结论:当![]() 时,式子有意义,
时,式子有意义,![]() ,对于
,对于![]() ,
,![]() 不能为负数.
不能为负数.
3.求值![]()
![]() 、
、![]() …
…
结论:当![]() 时,
时,![]() .
.
问:若根号内这个式子中的底数![]() ,根式还有意义吗?其值等于什么?
,根式还有意义吗?其值等于什么?
例如,![]() ,其中-2与2互为相反数;
,其中-2与2互为相反数;![]() ,其中-3与3互为相反数;
,其中-3与3互为相反数;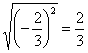 ,其中
,其中![]() 与
与![]() 互为相反数.
互为相反数.
【讲解新课】
提出问题:![]() 等于什么?引导学生讨论、猜测、联想,得到结论:
等于什么?引导学生讨论、猜测、联想,得到结论:
![]()
教师可结合学生的具体情况,将上面公式用最简练的语句表达,并反复提问中差学生,加深其印象,进一步提问:若![]() 时,
时,![]() 能否等于
能否等于![]() ,以增强学生的辨别能力,加强学生对公式的理解和记忆.
,以增强学生的辨别能力,加强学生对公式的理解和记忆.
例1 化简:
(1)![]() ; (2)
; (2)![]() .
.
解:(略).
注:![]() 可看作
可看作![]() ,把
,把![]() 先写为
先写为![]() ;
;
![]() 可看作
可看作![]() ,把
,把![]() 先写为
先写为![]() .
.
例2 化简:![]() .
.
分析:底数![]() 是非负数还是负数将直接影响结果,这时要注意条件,由条件
是非负数还是负数将直接影响结果,这时要注意条件,由条件![]() ,可得
,可得![]() .
.
∴![]() .
.
解:(略).
例3 化简下列各式:
(1)![]() (
(![]() ); (2)
); (2)![]() (
(![]() );
);
(3)![]() (
(![]() ); (4)
); (4)![]() (
(![]() ).
).
解:(1)∵![]()
∴ ![]() .
.
∴ ![]()
![]() .
.
(2)∵![]()
∴ ![]() ,即
,即![]() .
.
∴ ![]()
![]()
![]() .
.
(3)∵![]()
∴ ![]() ,即
,即![]() .
.
∴ ![]()
![]()
![]() .
.
(4)∵![]() ,
,
∵![]() ,即
,即![]() .
.
∴![]() .
.
注:要从条件出发,判断根号下面式子的底数是非负数还是负数,再根据公式![]() 计算出结果,因此在解题过程中,也是先写出条件,后进行变形,判断底数的正、负.
计算出结果,因此在解题过程中,也是先写出条件,后进行变形,判断底数的正、负.
在写解题步骤上,尽量完整,以减少失误,并训练学生的逻辑思维能力.
(二)随堂练习
1.求值:
(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() (
(![]() );
);
(4)![]() ;(5)
;(5)![]() .
.
解:(1)![]() .
.
(2)![]() .
.
(3)![]() .
.
(4)![]() .
.
(5)![]() .
.
注:![]() ,学生易与
,学生易与![]() 相混淆.
相混淆.
2.化简:
(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;
;
(4)![]() (
(![]() ); (5)
); (5)![]() (
(![]() ).
).
解:(1)![]() .
.
(2)![]() .
.
(3)![]() .
.
(4)![]() .
.
(5)![]() .
.
(三)总结、扩展
对公式![]() ,一定要在理解在基础上牢固掌握,要准确地运用公式进行二次根式的化简,关键是对根号内式子的底数的判断.
,一定要在理解在基础上牢固掌握,要准确地运用公式进行二次根式的化简,关键是对根号内式子的底数的判断.
(四)布置作业
教材p213中1(2)、(3);2(1)、(2).
(五)板书设计
标 题 1.复习题 4.练习题 2.公式 3.例题 |
中考 高考名著
常用成语