三角形的高、中线与角平分线 教学设计
§7.1.2三角形的高、中线与角平分线
【教学重点与难点】
教学重点：1．了解三角形的高、中线与角平分线的概念．
2．能利用三角形的高、中线和角平分线的性质进行简单计算．
教学难点：1．能用自己的语言说出三角形高、中线与角平分线的概念．
2．熟练运用三角形的高、中线和角平分线的性质进行有关计算．
【教学目标】
1．了解三角形的高、中线与角平分线的概念．毛
2．准确区分三角形的高、中线与角平分线．
3．能够独立完成与三角形的高、中线和角平分线有关的计算．
【教学方法】
以学生实践为主，在已学内容的基础上进行更进一步的探究，从而发现新的结论，以此培养学生发现和解决问题的能力．
【教学过程】
一．回顾旧知 提出问题
|
问题1：数一数，图中共有多少个三角形?请将它们全部用符号表示出来．
学生回答：图中共有5个三角形．
它们分别是：△ABC、△ABD、△ACD、
△ADE、△CDE．
问题2：利用长为3、5、6、9的四条线段可以组成几个三角形?为什么?
学生回答：可以组成2个三角形．
从四条线段中任选三条组成三角形，共有四种选法：①3、5、6，②3、5、9，③3、6、9，④5、6、9，其中，满足“三角形两边之和大于第三边”的只有第①、④这两组．
问题3：利用△ABC的一条边长为4cm，面积是24 cm2这两个条件，你能求出什么结论?
学生回答：能够求出的△ABC高是3 cm．
（教学说明：教师利用问题让学生回顾所学知识，特别是问题3内容的变化，可以引起学生注意和疑问，将学生的思路引入与三角形有关的线段中．）
二、探索新知 解决问题
1．通过作图探索三角形的高
（设计说明：通过经历画三角形的高的过程，使学生在头脑中留下清晰形象，并能结合这些具体形象叙述高的定义．）
|
学生画出三角形所有的高，观察这些高的特点．
问题2：根据画高的过程说明什么叫三角形的高?
学生讨论回答，师完善并归纳：从三角形的一个顶点向它的对边所在直线作垂线，连接顶点和垂足之间的线段称为三角形的高．
问题3：在这些三角形中你能画出几条高?它们有什么相同点和不同点?
学生回答：每个三角形都能画出三条高．
相同点是：三角形的三条高交于同一点．
不同点是：锐角三角形的高交于三角形内一点，直角三角形的高交于直角的顶 点，钝角三角形的高交于三角形外一点．
问题4：如图所示，如果AD是△ABC的高，你能得到哪些结论?
学生回答：如果AD是△ABC的高，则有：
AD⊥BC于D，∠ADB=∠ADC=90°．
（教学说明：三角形的高的概念在书中并没有具体给出，所以学生在归纳定义的时候会有一定的困难．那么在授课时就要留给学生充足的时间进行思考和讨论，教师可以引导学生先利用具体图形进行定义，再由具体图形中抽出准确、简明的语言，同时要强调：三角形的高是一条线段．在问题3中，有些学生会认为直角三角形只能画出斜边上的一条高，这时教师要给予讲解，说明另外两条直角边也是这个直角三角形的高．而问题4是要将三角形的高用符号语言表示出来，这是为以后学习证明打基础．）
2．类比探索三角形的高的过程探索三角形的中线
（设计说明：利用类比的方法进行探索，可以留给学生更多思考与探究的空间，有得于拓展学生的思维，培养学生自主探究的学习习惯．）
|
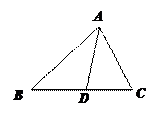学生回答：
．
问题2：如图，如果点D是线段BC的中点，那么线段AD就称为△ABC 的中线．类比三角形的高的概念，试说明什么叫三角形的中线?由三角形的中线能得到什么结论?
学生回答：三角形中连结一个顶点和它对边中的线段称为三角形的中线．
如果线段AD是△ABC的中线，那么
．
问题3：画出下列三角形的所有的中线，并讨论说明三角形的中线有什么特点?
|
学生回答：无论哪种三角形，它们都有三条中线，并且这三条中线都会交于一点，这一点都在三角形的内部．
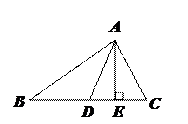问题4：如图所示，在△ABC中，AD是△ABC的中线，AE是△ABC的高．试判断△ABD和△ACD的面积有什么关系?为什么?
学生回答：△ABD和△ACD的面积相等．理由：
∵AD是△ABC的中线
∴BD=CD
∵AE既是△ABD的高，也是△ACD的高
∴
∴△ABD和△ACD的面积相等．
问题5：通过问题4你能发现什么规律?
学生回答：三角形的中线将三角形的面积平均分成两份．
（教学说明：让学生利用对三角形的高的探究过程，利用类比的方法进行对三角形的中线的探究．“类比思想”是数学学习中常用的一种思想，所以在授课过程中要让学生体会运用这种思想进行探究的好处，培养自主探究的能力．问题4和问题5的设立是对三角形中线的知识进行扩展，并不是教科书中的内容，但能够使学生更深刻地体会三角形中线的特点，同时，根据课堂时间的需要，对于这两个问题的讲授，教师可以自行调节．）
3．通过类比的方法探究三角形的角平分线
（设计说明：再次使用类比的方法进行探究，让学生经历动脑思考探索的过程，对知识有进一步的理解．）
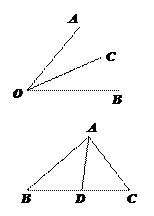
问题1：如图，若OC是∠AOB的平分线，你能得到什么结论?
学生回答：
．
问题2：如图，在△ABC中，如果∠BAC的平分线AD交BC边于点D，我们就称AD是△ABC的角平分线．类比探索三角形的高和中线的过程，你能得到哪些结论?三角形的角平分线与角的角平分线相同吗?为什么?
学生回答：三角形一个内角的平分线与它的对边相交，这个角的顶点与交点之间的线段称为三角形的角平分线．
三角形有三条角平分线，并且这三条角平分线在三角形内交于一点．
如果AD是△ABC的角平分线，那么就有
．
三角形的角平分线与一个角的角平分线不一样，三角形的角平分线是一条线段，有长度，而角的平分线是一条射线，没有长度．
（教学说明：对于三角形的角平分线的探究，教师要给学生足够的空间和时间，如果漏下了哪一点没有探究到，教师可以给予提示．）
三、巩固训练 熟练技能
（设计说明：通过比较练习，帮助学生掌握三角形的高、中线和角平分线的基本性质，熟练基本技能．）
练习1：如图，在△ABC中画出这个三角形的高BD，中线CE和角平分线BF．
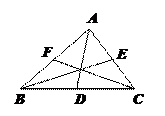
练习2：如图，已知AD，BE，CF都是△ABC的三条中线．
则AE= =
，BC=2 ，AF= ．
学生：CE，AC，BD或CD，BF．
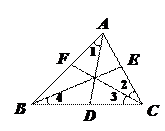练习3：如图，已知AD，BE，CF都是△ABC的三条角平分线．
则∠1= ，∠2= = ，
∠ABC=2 ．
学生：∠BAC，∠3，∠ACB，∠4或∠ABE．
练习3：如图，△ABC中，AC=12 cm，BC=18 cm，△ABC的高AD与BE的比是多少?
|
所以有
解得 
（教学说明：练习的设计以基础知识为主，要让学生独立完成．而练习3是所学知识的一个应用，要让学生有利用面积求高的意识，开阔思路．）
四、反思总结 情意发展
（设计说明：围绕三个问题，师生以谈话交流的形式，共同总结本节课的学习收获。）
问题1：本节课你学习了什么?
问题2：本节课你有哪些收获?
问题3：通过今天的学习，你想进一步探究的问题是什么?
（教学说明：以上设计再次通过对三个问题的思考引导学生回顾自己的学习过程，畅所欲言，加强反思、提炼及知识的归纳，纳入自己的知识结构）
五、课堂小结
1．本节主要学习三角形的高、中线和角平分的概念与性质．
2．本节涉及到的思想方法是类比思想．
3．注意的问题：
（1）每个三角形都有三条高，三条中线和三条角平分线．
（2）三角形的三条高交于一点，但锐角三角形的高交于三角形内一点，直角三角形的高交于直角的顶点，钝角三角形的高交于三角形外一点．三角形的三条中线交于三角形内一点，三角形的三条角平分线也交于三角形内的一点．
（3）三角形的高、中线和角平分线都是线段．
（4）能将三角形的面积平均分成两部分的线是三角形的中线．
六、布置作业
1、课本69页习题7.1的3、4；
（教学说明：及时作业是巩固课堂学习知识的重要环节，练习题是对本节的基础知识进行巩固．）
七、拓展练习
（设计说明：在学习基础知识的基础上，拓展学生思维，提高学生的学习兴趣。）
|
求顶点C到边AB的高．
学生：解：设顶点C到边AB的高为h，由三角形的面积公式可得
，
所以有
，
解得：h=4.8
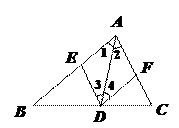所以，顶点C到边AB的高为4.8．
练习2：如图，在△ABC中，AD是角平分线，DE//AC，DF//AB．试判断∠3和∠4的关系，并说明理由．
学生：解：∠3=∠4．
理由：∵AD平分∠BAC，
∴∠1=∠2，
又∵DE//AC，DF//AB，
∴∠1=∠4，∠2=∠3
∴∠3=∠4．
练习3：利用所学知识将三角形分成面积相等的四部分．（至少画出4种）
|
学生：利用三角形中线的性质可得
|
……（教学说明：这三个练习是三角形的高、中线和角平分线的应用，特别是练习2，加入了平行线的性质，所以教师应给学生一定的思考时间，并让学生充分的合作交流，共同解决问题．）
【评价与反思】
本节内容是七年级数学第七章的第二节，主要介绍三角形的高、中线和角平分线的概念及基本性质，虽是一节概念教学课，但重点却在性质的应用上．
本节的知识内容较多，不仅要让学生了解三角形的高、中线和角平分线的概念，还要对这三种线段的表示方法和性质进行探究．在教学过程中，教师引导学生从熟悉的知识入手，并利用类比的方法自主探索新的知识．在教学过程中，教师应让学生以独立思考为主，并在必要时进行互助交流，让学生经历得出结论的过程，培养学生解决问题的能力．
在教学设计上，关注学生自主学习、合作交流的过程，让学生体会类比思想在探索新知中的作用，使学生在亲自经历整个探究过程后，能够对三角形的高、中线和角平分线的概念及性质有更好的理解，在获得数学活动经验的同时，提高探究、发现和创新的能力．
中考 高考名著
常用成语