正弦和余弦1 人教课标九年级下册
一、教学目标
1．使学生初步了解正弦、余弦概念；能够较正确地用
、
表示直角三角形中两边的比；熟记特殊角30°、45°、60°角的正、余弦值，并能根据这些值说出对应的锐角度数.
2．逐步培养学生观察、比较、分析、概括的思维能力.
3．渗透教学内容中普遍存在的运动变化、相互联系、相互转化等观点.
二、学法引导
1．教学方法：指导发现探索法.
2．学生学法：自主、合作、探究式学习.
三、重点、难点、疑点及解决方法
1．教学重点：使学生了解正弦、余弦概念.
2．教学难点：用含有几个字母的符号组
、
表示正弦、余弦；正弦、余弦概念.
3．疑点：锐角的正弦、余弦值的范围.
4．解决办法：通过旧知创设情境，采用从特殊到一般的方法，引导学生进行探究式学习，从而解决重难点及疑点.
四、教具准备
三角板一副
五、教学步骤
（一）明确目标
1．引导学生回忆“直角三角形锐角固定时，它的对与斜边的比值、邻边与斜边的比值也是固定的.”
2．明确目标：这节课我们将研究直角三角形一锐角的对边、邻边与斜边的比值—正弦和余弦.
（二）整体感知
当直角三角形有一锐角为30°时，它的对边与斜边的比值为
，只要知道三角形任一边长，其他两边就可知.
而上节课我们发现，只要直角三角形的锐角固定，它的对边与斜边、邻边与斜边的比值也固定，这样只要能求出这个比值，那么求直角三角形未知边的问题也就迎刃而解了.
通过与“30°角所对的直角边等于斜边的一半”相类比，学生自然产生想学习的欲望，产生浓厚的学习兴趣，同时对以下要研究的内容有了大体印象.
（三）教学过程
正弦、余弦的要领是全章知识的基础，对学生今后的学习与工作都十分重要，因此确定它为本课重点，同时正、余弦概念隐含角度与数之间具有一一对应的函数思想，又用含几个字母的符号组来表示，因此概念也是难点.
在上节课研究的基础上，引入正、余弦，“把对边、邻边与斜边的比值称做正弦、余弦”.如图
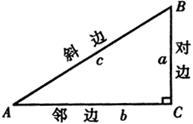
请学生结合图形叙述正弦、余弦定义，以培养学生概括能力及语言表达能力，教师板书：在
中，
为直角，我们把锐角
的对边与余边的比叫做
的正弦，记作
，锐角
的邻边与斜边的比叫做
的余弦，记作
.
.
若把
的对边
记作
，邻边
记作
，斜边
记作
，则
，
.
引导学生思考：当
为锐角时，
、
的值会在什么范围内?得结论
，
（
为锐角），这个问题对于较差学生来说有些难度，应给学生充分思考时间，同时这个问题也使学生将数与形结合起来.
教材例1的设置是为了巩固正弦概念，通过教师示范，使学生会求正弦，这里不妨增问“
、
”，经过反复强化，使全体学生都达到目标，更加突出重点.
【例1】求出如下图所示的
中的
、
和
、
的值.
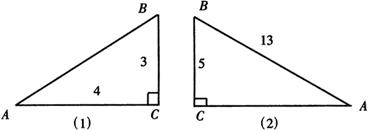
解：（1）∵斜边
，
∴
，
．
，
．
（2）
，
．
，
∴
，
．
学生练习教材p6～7中1、2、3题．
让每个学生画含30°、45°的直角三角形，分别求
、
、
和
、
、
.这一练习既用到以前的知识，又巩固正弦、余弦的概念，经过学习亲自动笔计算后，对特殊角三角函数值印象很深刻.
，
，
．
，
，
．
【例2】求下列各式的值：
（1）
；（2）
．
解：（1）
．
（2）
．
这了使学生熟练掌握特殊角三角函数值，这里还应安排六个小题：
（1）
；（2）
；
（3）
；（4）
．
（5）若
，则锐角
.
（6）若
，则锐角
.
在确定每个学生都牢记特殊角的三角函数值后，引导学生思考，“请大家观察特殊角的正弦和余弦值，猜测一下，
大概在什么范围内，
呢?”这样的引导不仅培养学生的观察力、注意力，而且培养学生勇于思考、大胆创新的精神，还可以进一步请成绩较好的同学用语言来叙述“锐角的正弦值随角度增大而增大，余弦值随角度增大而减小”.
（四）总结、扩展
首先请学生作小结，教师适当补充，“主要研究了锐角的正弦、余弦概念，已知直角三角形的两边可求其锐角的正、余弦值，知道任意锐角A的正、余弦值都在0～1之间，即
，
（
为锐角）．
还发现
的两锐角
、
，
，
，正弦值随角度增大而增大，余弦值随角度增大而减小”.
六、布置作业
教材p10中2，3.
预习下一课内容.
补充：（1）若
，则锐角
．
（2）若
，则锐角
．
七、板书设计
中考 高考名著
常用成语