多项式函数的导数 人教选修

教学目的：会用导数的运算法则求简单多项式函数的导数

教学重点：导数运算法则的应用

教学难点：多项式函数的求导

一、复习引入

1、已知函数，由定义求

2、根据导数的定义求下列函数的导数：

（1）常数函数 （2）函数

二、新课讲授

1、两个常用函数的导数：

2、导数的运算法则：

如果函数有导数，那么

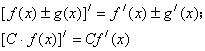
也就是说，两个函数的和或差的导数，等于这两个函数的导数的和或差；常数与函数的积的导数，等于常数乘函数的导数.

例1：求下列函数的导数：

（1） （2） （3）

（4） （5）为常数)

例2：已知曲线上一点，求：

（1）过点p的切线的斜率； （2）过点p的切线方程.

三、课堂小结：多项式函数求导法则的应用

四、课堂练习：1、求下列函数的导数：

（1） （2） （3） （4）

（5） （6）

2、已知曲线上有两点A（4，0），B（2，4），求：

（1）割线AB的斜率；（2）过点A处的切线的斜率；（3）点A处的切线的方程.

3、求曲线在点M（2，6）处的切线方程.

五、课堂作业

1、求下列函数的导数：

（1） （2） （3）

（4）（5） （6）

（7） （8）

（9） （10）

2、求曲线在处的切线的斜率。

3、求抛物线在处及处的切线的方程。

4、求曲线在点p（2，－3）处的切线的方程。