倍角公式教学设计 人教必修

教学目标

1．使学生能够导出二倍角的正弦、余弦、正切公式．

2．使学生能够正确运用二倍角公式化简三角函数式，求某些角的三角函数值，证明三角恒等式，并推导三倍角的正弦、余弦、正切公式．

3．通过以上公式的推导，学生能够了解各公式间的内在联系，从而培养学生推导公式的能力及辩证唯物主义观点．

教学重点与难点

教学重点是二倍角公式的推导、记忆及成立的条件．教学难点是灵活理解“二倍角”的含义，并熟练地解决有关问题．

教学过程设计

师：前几节课我们学习了两角和与差的三角函数，有几个非常重要的公式，请同学们回忆一下．

生：sin（α＋β）=sinα·cosβ＋cosα·sinβ．

sin（α-β）=sinα·cosβ-cosα·sinβ．

cos（α＋β）=cosα·cosβ-sinα·sinβ．

cos（α-β）=cosα·cosβ＋sinα·sinβ．

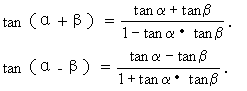
师：说得很准确．上面这几个公式随着我们学习的深入，大家会愈发体会到它们的重要性，因为它们是本章各类公式的基础．这章公式虽然较多，但只要掌握了它们之间的内在联系．就能既快又准地记住．以上六个公式的内在联系可以用下表来表示：

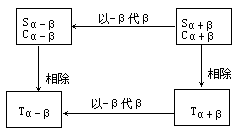
（教师在画上表图时，一定要强调公式成立的条件，对不能用公式的问题要转化用其它方法解决，例如诱导公式等．）

师：下面请同学们共同思考一个问题，如何用sinα，cosα，tanα来表示sin2α，cos2α，tan2α？

生：可以利用前面学过的两角和与差的三角函数公式，当两个角相等，即α＝β时，问题就解决了，例如：

sin 2α＝sin（α＋α）＝sinα·cosα＋cosα·sinα＝2sinα·cosα．

师：想得非常好．这正是老师多次向同学们强调的学好数学的八字方针，即“联想、对比、转化、应用”．在这个题目中的具体应用．这正是我们今天要学习的三角函数中很重要的一节的内容——二倍角的正弦、余弦、正切．

（教师板书课题，并请另一位学生叙述二倍角正弦、余弦、正切公式，用红粉笔写在黑板上．）

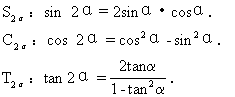
师：由推导过程可知，二倍角的三角函数公式是两角和的三角函数公式的特殊情况，大家在记忆时应注意公式间的联系．另外，由同角的三角函数关系sin2α＋cos2α＝1，公式C2α又可以变形为：

cos2α＝2cos2α-1

（要求学生在笔记本上推导过程．）

师：有了这组二倍角三角函数公式，我们是否就可以放心大胆地应用呢？

生：不行．还应考虑公式成立的条件．

师：非常好．我们在前面的两角和与差的三角函数公式中也遇到了类似的问题，请同学们联想前面的知识，讨论一下二倍角三角函数公式成立的条件．（这也是本节的教学重点．）

（给些时间请学生讨论，得结论．）

生：在二倍角的正弦和余弦公式中，角α没有限制，即α为任意角．但

∈Z时，公式才能成立，否则公式不成立．

师：你能阐述一下你的理由吗？

kπ，k∈Z时，tan2α是不存在的．因此以上两种情况均不能使用二倍角正切公式．

师：说得非常好．想得全面，说得充分．但我还有一个问题希望同

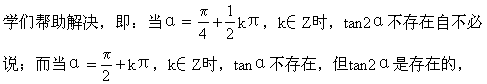
刚才同学说不能用二倍角正切公式解决，那又如何处理呢？

生：这种情况，可以改用诱导公式

师：考虑问题要周全，处理问题要讲究方法，要学会作多面手，善于运用所学的知识，用不同的方法来解决问题．通过我们的讨论，使二倍角公式趋于完善，大家运用起来得心应手，请大家将二倍角三角函数公式成立的条件写在公式后面．

（教师用红粉笔写在黑板上．）

师：在同学们熟悉了二倍角公式的基础上，我还有几点说明希望同学们注意．

第一，公式是用单角三角函数来表达二倍角的三角函数．

第二，要灵活理解“二倍角”的含义．二倍角公式不仅限于2α是

例

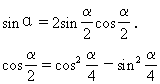
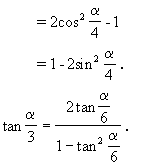
第三，一般情况下sin2α≠2sinα，当且仅当α＝kπ，k∈Z时，sin2α＝2sinα成立．同理，一般情况下，cos2α≠2cosa，tan2α≠2tanα．我留一个课下思考题，请同学们研究在什么条件下它们才能成立．下面请同学们看投影．

（事先将例题在幻灯片上写好，这样节省时间，提高课堂密度．）

例1不查表，求下列函数值：

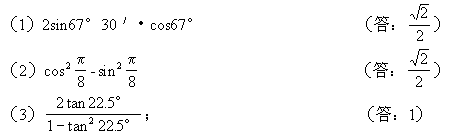
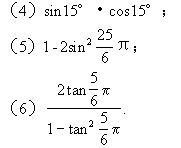
（可将（1）～（3）作为第1组，请学生起立直接口答；（4）～（6）作为第2组，在笔记本上写出求值过程．注意每一步均要体现运用公式的变形过程，不要跳步．）

（（1）～（3）题过程略，（4）～（6）题学生做完后起立说，教师板书．）

师：要熟悉二倍角公式，尤其是多种形式的两个角的倍数关系，还要注意公式的正用与反用，注意恒等变形。

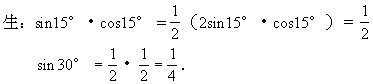
生：第（5）题有两种方法：

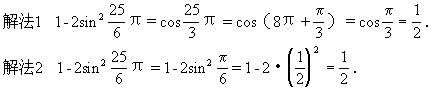
生：第（6）题也有两种变形方法，

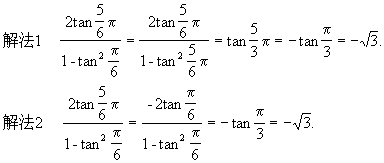
师：上面两个题两位同学做得都很好，我们在做题时要讲究一题多解，多题一解，多解归一．要做到这些是很不容易的，要求大家在平时作业中，课堂练习中有意识地培养锻炼自己，这也是注重知识间联系，真正做到将知识融会贯通的一条重要途径．

师：（板书）

例2

师：题目中对角α有范围限制，做题中应注意什么？仅知sinα值，欲求二倍角正弦、余弦、正切，先需要知道什么？请大家带着问题想一想．

生：角α有范围限制，应考虑三角函数的符号；知道sinα值，还需求出cosα，tanα才能完成题目要求．

师：你说我写．请全体同学看看他的解题过程，有问题可以指出来．

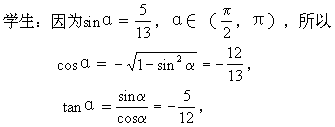
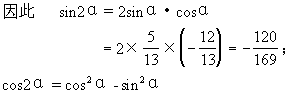
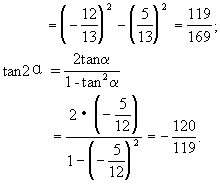
师：首先肯定最终的结果是正确的．但过程有没有值得商榷的地方？

简化求解过程．

生：我想cos2α＝cos2α-sin2α，走这条路固然可以，但还是用cos2α＝1-2sin2α较好，这样使用已知的原始数据，减少了错误的可能性．

师：两位同学说得非常好．答案正确是我们最低的要求，对自己标准要高一些，要精益求精，我们师生以此共勉吧！我这里有一道证明题，请全体同学充分发挥你的聪明才智，战胜它，并力争一题多解．

师：（板书）

例3

（给学生一些时间思考．）

师：请大家想想，到现在为止，证明三角恒等式我们大致有几种方法？

生：从复杂一端化向简单一端；两边化简，中间碰头；化切割为弦；还可以利用分析综合法解决．有时几种方法会同时使用．

师：概括得很好．有没有补充？

生：今天学习了二倍角公式，我认为可以化倍角为单角，这也是证明三角恒等式的一种方法．

师：非常好．他很善于运用所学的新知识，我们大家要向他学习．下面希望同学踊跃发言，把你的方法展示给大家．

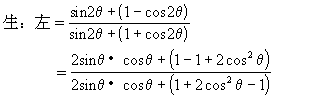
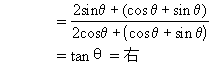
生：我和前面同学的方法略有区别．

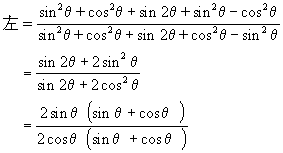
=tanθ=右．

师：两位同学在前期的化简方法不同，变形都很巧妙．同学们从中是否体会到了数字“1”的妙用？它在三角恒等式中一旦出现，在证明过程中就会起到至关重要的作用，在今后的证题中，万万不要忽视它．

生：老师，我对“1”的妙用深有体会，下面我说说我的证明过程．

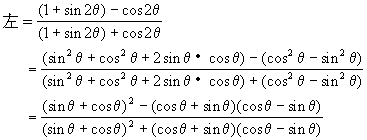
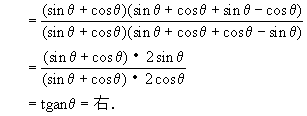
教师：思路很清晰．以上几种方法大致遵循以下规律：首先从复杂端化向简单端；第二，化倍角为单角，这是我们今天刚刚学习的；第三，证题中注意对数字的处理，尤其“1”的妙用，还望同学们仔细体会．在这道题中通常用的几种方法大家都见到了，我想留一个思考题：能够将右端的正切化成弦，再用分析法，能够证出该题．课下请同学们思考．倍角公式不限于二倍角，凡用单角的三角函数来表示的三倍角，四倍角等的三角恒等式，都叫做倍角公式．下面我们来试着推导三倍角的正弦、余弦、正切公式．

师：（板书）

例4（1）用sinθ表示sin3θ；

（2）用cosθ表示cos3θ．

（给一点时间让学生思考．）

师：面对一道新题，怎么想？从哪里入手？怎么变形？能否利用所学的知识解决它？其实就是要学会“联想”，不要害怕因此而耽误时间，久而久之，你们倘若真正养成了会想问题的好习惯，你的数学水平，不，应该是整体各科的水平，就会上升一个大台阶，对你们将来步入社会，继续发展是大有好处的．

生：可以将三倍角先转化成二倍角和单角，再将二倍角转化成单角，这样问题就可以解决了．

师：思路是对的，能否具体说一下？

生：sin3θ=sin（2θ＋θ）

=sin2θ·cosθ＋cos2θ·sinθ

=2sinθ·cosθ·cosθ＋（1-2sin2θ）·sinθ．

（停顿．问他为什么用cos2θ=1-2sin2θ，而不用另外两种形式．）

（续上）=2sinθ·cos2θ＋sinθ-2sin3θ

=2sinθ（1-sin2θ）＋sinθ-2sin3θ

=3sinθ-4sin3θ．

所以sin3θ=3sinθ-4sin3θ．

师：推导得非常漂亮，每一步变形均很清楚，格式很标准．下面请一位同学上黑板推导三倍角的余弦公式．

生：cos3θ=cos（2θ＋θ）

=cos2θ·cosθ-sin2θ·sinθ

=（2cos2θ-1）cosθ-2sin2θ·cosθ

=2cos3θ-cosθ-2（1-cos2θ）·cosθ

=4cos3θ-3cosθ．

所以cos3θ=4cos3θ-3cosθ．

师：推导正确．上面我们是由和角公式与二倍角公式结合使用，推出结论，哪位同学还有其它方法？

生：老师，我只用了和角公式就直接推出来了，以三倍角正弦为例．

sin（α＋β＋γ）

=sin[（α＋β）＋γ]

=sin（α＋β）·cosγ＋cos（α＋β）·sinγ

=[sinα·cosβ＋cosα·sinβ]·cosγ＋[cosα·cosβ-sinα·sinβ]·sinγ

=sinα·cosβ·cosγ＋cosα·sinβ·cosγ＋cosα·cosβ·sinγ-sinα·sinβ·sinγ．

当α=β=γ=θ时，即得：

sin3θ=sinθ·cos2θ＋sinθ·cos2θ＋sinθ·cos2θ-sin3θ

=3sinθ·cos2θ-sin3θ

=3sinθ（1-sin2θ）-sin3θ

=3sinθ-4sin3θ．

用此方法，同样可以推出三倍角余弦公式．

师：刚才我发现有的同学在兴奋地点头，继而又微微摇头，有什么见解？

生：方法2同样是一种推导方法，但与方法1比较，还是麻烦些，所以我认为，求其它倍角公式时，还是把和角公式与倍角公式结合起来用比较简便．

师：说得很有道理．我们要力争对每种方法作深入的探讨，这样将加深对题目本质的理解，加深对每种解法本质的理解．加深对所用概念、公式和相互联系的理解．如果将这些解法相互比较，进行抽象，还会在方法上有所创造，提高解题能力，那就更有价值了．

师：（板书）．用tanθ表示tan3θ．

这个作为思考题，同学们回家推导一下．我们回顾一下所学过的内容．

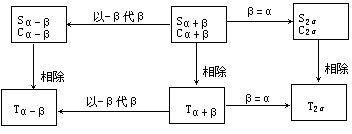
（在复习两角和与差的三角函数公式的表图上，扩充倍角公式，使学生认清它们之间的内在联系．）

作业：课本p219练习第3，4，5，7题．

补充：不查表，用倍角公式求sin18°的值．

课堂教学设计说明

这份教案写的是倍角公式一堂课的实录，以问答的形式，详细地叙述出来．如果只是为了自己教学，我想，只要记下教学过程即可：

1．复习两角和与差的三角函数公式．

2．引入并推导二倍角公式及其变形．

3．讨论二倍角公式成立的条件．

4．强调灵活理解二倍角的含义．

5．例1、例2是熟悉公式，强调书写格式．

6．例3、例4是强调一题多解，从而上升至类比和化归的思想．

7．小结，作业．

我为什么要采取上面几个环节呢？目前数学教材是从少数公理、定理出发，通过演绎，将知识展开．于是过程1，3，4可省略，直接给出二倍角公式，继而大量练题．教材总是把知识和方法用定论的形式直接呈现在学生面前，新旧知识的衔接点直接给出，学生只要记住公式就行．因此这种做法的优点是直截了当，节约时间；缺点是学生缺乏一个完整的认识过程，把知识或方法不是作为“过程”，而是作为“结果”直接抛给学生，长此以往，越“抛”越多，学生头脑中很难形成一个有效的认识结构．反之，插入环节1，3，4，使学生真正掌握二倍角公式的本质，知其然，还知其所以然，就为今后继续学习三角公式打下良好的基础，也为构造全章三角公式的内在联系图创造了条件，这也是学好这部分知识的关键．

为了调动学生的积极性，发挥学生的主体作用，从一上课开始，到推导公式，几道例题始终把解决问题的机会留给学生．在每一部分又分别强调学法指导，一题多解，善于联想，举一反三，善于总结，整个教学过程又是在教师的指导下进行的，使得教师的主导作用和学生的主体作用十分融洽．学生不会因为感到枯燥而厌学，反而会全身心地投入到课堂上，我们的教学目的也就达到了．