三角恒等变换 小结复习2,3 人教必修

教学目标

(一)知识目标

1.任意角的概念、弧度制、任意角的三角函数的概念、同角三角函数间的关系、诱导公式；

2.两角和与差的三角函数、二倍角的三角函数；

3.三角函数的图象和性质、已知三角函数值求角.

(二)能力目标

1.理解任意角的概念、弧度的意义；能正确地进行弧度与角度的换算；

2.掌握任意角的正弦、余弦、正切的定义，并会利用与单位圆有关的三角函数线表示正弦、余弦和正切；了解任意角的余切、正割、余割的定义；掌握同角三角函数的基本关系式；掌握正弦、余弦的诱导公式；

3.掌握两角和与两角差的正弦、余弦、正切公式；掌握二倍角的正弦、余弦、正切公式；

4.能正确运用三角公式，进行三角函数式的化简、求值及恒等式证明；

5.会用与单位圆有关的三角函数线画出正弦函数、正切函数的图象，并在此基础上由诱导公式画出余弦函数的图象；理解周期函数与最小正周期的意义；并通过它们的图象理解正弦函数、余弦函数、正切函数的性质；会用“五点法”画正弦函数、余弦函数和函数y＝Asin(ωx＋<…)的简图，理解A、ω、…的物理意义；

6.会用已知三角函数值求角，并会用符号arcsinx、arccosx、arctanx表示.

(三)德育目标

1.渗透“化归”思想；

2.培养逻辑推理能力；

3.提高解题能力.

教学重点

三角函数公式、三角函数(尤其是正弦函数、余弦函数、正切函数)的图象和性质的应用.

教学难点

灵活应用三角公式，正弦、余弦、正切函数的图象和性质解决问题.

教学方法

讲练结合法

通过讲解强化训练题目，加深对三角函数知识的理解，提高对三角函数知识的应用能力.

教学过程

A组

1.解：(1)Z}，

(2)Z}，

(3)Z}，

(4)Z｝，－2π，0，2π

评述：这一题目要求我们首先要准确写出集合S，并判断k可取何值时，能使集合S中角又属于所要求的范围.

2.解：由l＝｜α｜r得

cm

cm²

答：周长约44 cm，面积约1．1×10 cm²

评述：这一题需先将54°换算为弧度数，然后分别用公式进行计算.

3.(1)sin4＜0；(2)cos5＞0；(3)tan8＜0；(4)tan(－3)＞0．

评述：先判断角所属象限，然后确定其三角函数的符号..

评述：先由已知条件确定角所属象限，然后结合同角三角函数基本关系式，求出另外的三角函数值.

5.解：由sinx＝2cosx，得tanx＝2

∴x为第一象限或第三象限角

当x为第一象限角时

tanx＝2，cotx＝，cosx＝，secx＝，sinx＝，cscx＝

当x为第三象限角时

tanx＝2，cotx＝，cosx＝－，secx＝－，sinx＝－，cscx＝－

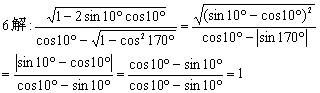
评述：注意灵活使用同角三角函数的基本关系式的变形式，即“1”的妙用，这也是三角函数式化简过程中常用的技巧之一，另外，注意及时使用诱导公式和三角函数图象和性质：当α∈［0,)时，sinα＜cosα.

7.解：sin⁴α－sin²α＋cos²α＝sin²α(sin²α－1)＋cos²α＝(1－cos²α)(－cos²α)＋cos²α

＝－cos²α＋cos⁴α＋cos²α＝cos⁴α

评述：注意使用sin²α＋cos²α＝1及变形式.

8.证明：(1)左边＝2(1－sinα)(1＋cosα)＝2(1－sinα＋cosα－sinαcosα)

＝2－2sinα＋2cosα－sin2α

右边＝(1－sinα＋cosα)2＝［1－(sinα－cosα)］2

＝1－2(sinα－cosα)＋(sinα－cosα)2

＝1－2sinα＋2cosα＋sin2α＋cos2α－2sinαcosα

＝2－2sinα＋2cosα－sin2α

∴左边＝右边

即原式得证.

(2)左边＝sin²α＋sin²β－sin²α·sin²β＋cos²α·cos²β

＝sin²α(1－sin²β)＋cos²α·cos²β＋sin²β

＝sin²α·cos²β＋cos²α·cos²β＋sin²β

＝cos2β(sin2α＋cos2α)＋sin2β＝1＝右边

∴原式得证

评述：三角恒等式的证明一般遵循由繁到简的原则.

9.解：(1)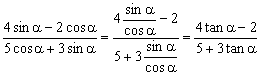

将tanα＝3代入得，原式＝

(2)sinαcosα＝tanα·cos2α＝tanα·

(3)(sinα＋cosα)2＝1＋2sinαcosα＝1＋2×

评述：注意挖掘已知条件与所求结论中的三角函数的关系.

10.解：(1)sinπ＋cosπ＋tan(－π)＝sin＋cos－tan=

(2)sin2＋cos3＋tan4≈1．0777

评述：注意灵活应用诱导公式化简后再求值.

11.解：(1)∵sin(π＋α)＝－＝－sinα

∴sinα＝

∴cos(2π－α)＝cosα＝±

当α为第一象限时，cosα＝

当α为第二象限时，cosα＝－

(2)tan(α－7π)＝－tan(7π－α)＝tanα

当α为第一象限时，tanα＝

当α为第二象限时，tanα＝－

评述：要注意讨论角的范围.

12.解：(1)sin378°21′＝sin18°21′＝0．3148

(2)sin(－879°)＝－sin(159°)＝－sin21°＝－0．3584

(3)sin3＝0．1409

评述：要用诱导公式将其转化为锐角三角函数值问题.

13.解：设0＜x＜2π

14.解：∵cosα＝－且π＜α＜

∴sinα＝－，∴tanα＝

∴tan(－α)＝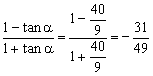

评述：仔细分析题目，要做到有的放矢.

15.解：∵sinα＝，α为锐角 ∴cosα＝

又∵sinβ＝，β为锐角 ∴cosβ＝

∴cos(α＋β)＝cosαcosβ－sinαsinβ＝

又∵0＜α＋β＜π，∴α＋β＝

说明：若先求出sin(α＋β)＝，则需否定α＋β＝.

评述：一般地，若所求角在(0，π)上，则一般取此角的余弦较为简便；若所求角在(－，)上，则一般取此角的正弦较为简便.

16.(1)证明：∵

∴tan(A＋B)＝tan＝1＝

即：tanA＋tanB＝1－tanAtanB

∴tanA＋tanB＋tanAtanB＝1

∵(1＋tanA)(1＋tanB)＝1＋tanA＋tanB＋tanAtanB

∴(1＋tanA)(1＋tanB)＝2

(2)证明：由(1＋tanA)(1＋tanB)＝2得

tanA＋tanB＝1－tanAtanB

又∵0＜A＜，0＜B＜

∴tanA＋tanB＞0

即tan(A＋B)＝1

又∵0＜A＋B＜π

∴A＋B＝

(3)解：由上述解答过程可知：

两锐角之和为直角之半的充要条件是(1＋tanA)(1＋tanB)＝2不可以说“两个角A、B之和为的充要条件是(1＋tanA)(1＋tanB)＝2”因为在(2)小题中要求A、B都是锐角.

17.证明：设正方形的边长为1

则tanα＝，tanβ＝

∴tan(α＋β)＝

又∵0＜α，β＜π，∴α＋β＝

评述：要紧扣三角函数定义.

18.证明：∵0＜α，β，γ＜

且tanα＝＜1，tanβ＝＜1，tanγ＝＜1

∴0＜α，β，γ＜

又∵tan(α＋β＋γ)＝1

0＜α＋β＋γ＜

∴α＋β＋γ＝45°

20.解：设△ABC的底为a，则腰长为2ａ

∴sin＝ cos＝

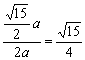
∴sinA＝2sincos＝

cosA＝2cos2－1＝－1＝

tanA＝．

21.证明：p＝ｉｖ＝ｉｍsinωｔ·ｖｍsin(ωｔ＋)＝ｉｍｖｍsinωｔcosωｔ＝ｉｍｖｍsin2ωｔ

22.证明：由题意可知：

sin＝

cos＝

∴sinθ＝2sincos＝2··＝

23.解：由教科书图4—12，可知：

当α为某一象限角时，有：

｜sinα｜＝｜Mp｜，｜cosα｜＝｜OM｜

∵｜Mp｜＋｜OM｜＞｜Op｜＝1，

∴｜sinα｜＋｜cosα｜＞1

当α的终边落在坐标轴上时，有｜sinα｜＋｜cosα｜＝1．

因此，角α的正弦绝对值与余弦绝对值之和不小于1.

评述：要注意数形结合这种重要的数学思想的利用.

24.解：(1)由1－tanx≠0，得tanx≠1

∴x≠kπ＋且x≠kπ＋，k∈Z

∴函数y＝的定义域为：

｛x｜x≠kπ＋且x≠kπ＋，k∈Z｝

(2)由≠kπ＋得x≠2kπ＋π，k∈Z

∴y＝tan的定义域为｛x｜x≠2kπ＋π，k∈Z｝

25.解：(1)由cos2x＝1．5，得cosx＝±

又∵ ［－1，1］

∴cos2x＝1．5不能成立.

(2)由sinx－cosx＝sin(x－)∈［－，］

∴sinx－cosx＝2．5不能成立

(3)当x＝时，tanx＝1

∴tanx＋＝2有可能成立

(4)由sin3x＝－得sinx＝－∈［－1，1］

∴sin3x＝－成立.

评述：要注意三角函数的有界性.

26.解：(1)当sinx＝1时，即x＝2kπ＋，k∈Z时,

y＝＋取得最大值.

∴y＝＋的最大值为＋.

使y取得最大值的x的集合为｛x｜x＝＋2kπ，k∈Z｝.

当sinx＝－1时，即x＝－＋2kπ时.

y＝＋取得最小值.

∴y＝＋的最小值为－.

使y取得最小值的x的集合为｛x｜x＝－＋2kπ，k∈Z｝.

(2)当cosx＝－1即x＝(2k＋1)π时,

y＝3－2cosx取得最大值,

∴y＝3－2cosx的最大值为5.

使y取得最大值的x的集合为｛x｜x＝2kπ＋π，k∈Z｝.

当cosx＝1，即x＝2kπ时

y＝3－2cosx取得最小值

∴y＝3－2cosx的最小值为1

使y取得最小值的x的集合为｛x｜x＝2kπ，k∈Z｝

27.解：(1)y＝sinx－cosx(x∈R)＝2sin(x－)，

∴ymax＝2，ymin＝－2

(2)y＝sinx＋cosx＝sin(x＋)，(x∈R)

∴ymax＝，ymin=－

28.解：当0≤x≤2π时，由图象可知：

(1)当x∈［，2π］时，角x的正弦函数、余弦函数都是增函数.

(2)当x∈［，π］时，角x的正弦函数、余弦函数都是减函数.

(3)当x∈［0，］时，角x的正弦函数是增函数，而余弦函数是减函数.

(4)当x∈［π，］时，角x的正弦函数是减函数，而余弦函数是增函数.

29.解：(1)由f(－x)＝(－x)2＋cos(－x)＝x2＋cosx＝f(x)

得y＝x2＋cosx，x∈R是偶函数

(2)由y＝｜2sinx｜＝｜2sin(－x)｜

得y＝｜2sinx｜，x∈R是偶函数

(3)由y＝tanx2＝tan(－x)2

得y＝tanx2，x≠±(k∈Z)是偶函数

(4)由y＝x2sinx＝－(－x)2sin(－x)

得y＝x2sinx，x∈R是奇函数

30.(1)y＝sin(3x－)，x∈R

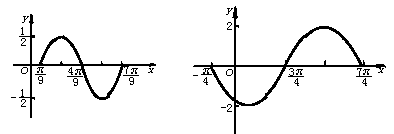
(2)y＝－2sin(x＋)，x∈R

(3)y＝1－sin(2x－)，x∈R

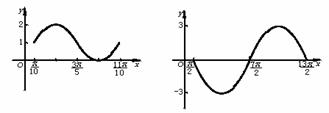
(4)y＝3sin(－)，x∈R

31.(1)略

(2)解：由sin(π－x)＝sinx，可知函数y＝sinx，x∈［0，π］的图象关于直线x＝对称，据此可得出函数y＝sinx，x∈［，π］的图象；又由sin(2π－x)＝－sinx，可知函数y＝sinx，x∈［0，2π］的图象关于点(π，0)对

称，据此可得出函数y＝sinx，x∈［π，2π］的图象.

(3)解：把y轴向右(当 ＞0时)或向左(当 ＜0时＝平行移动｜ ｜个单位长度，再把x轴向下(当k＞0时)或向上(当k＜0时＝平移｜k｜个单位长度，就可得出函数y＝sin(x＋)＋k的图象.

32.解：(1)y＝sin(5x＋)，x∈R振幅是1，周期是，初相是

把正弦曲线向左平行移动个单位长度，可以得出函数y＝sin(x＋)，x∈R的图象；再把所得图象上所有点的横坐标缩短到原来的倍(纵坐标不变)，就可得出函数y＝sin(5x＋)，x∈R的图象.

(2)y＝2sinx，x∈R

振幅是2，周期是12π，初相是0

把正弦曲线上所有点的横坐标伸长到原来的6倍(纵坐标不变)，可以得出函数y＝sinx，x∈R的图象；再把所得图象上所有点的纵坐标伸长到原来的2倍(横坐标不变)，就可得出函数y＝2sinx，x∈R的图象.

33.解：(1)由ｈ＝2sin(ｔ＋)，ｔ∈［0，＋∞）

得ｔ＝0时，ｈ＝cm

即：小球开始振动时的位置在离平衡位置cm处.

(2)当sin(ｔ＋)＝1时，ｈmax＝2sin(ｔ＋)＝－1时，ｈmax＝－2

即：小球最高、最低点与平衡位置的距离都是2 ｃｍ.

(3)由T＝得T＝2πs

即：经过2πs，小球往复振动一次.

(4)f＝

即：小球每1 s往复振动次.

34.解：(1)由sinx＝0，x∈［0，2π］ 得x＝0，π，2π

(2)由cosx＝－0．6124，x∈［0，2π］

得x＝0．71π，1．29π或arccos(－0．6124)，2π－arccos(－0．6124)

(3)由cosx＝0，x∈［0，2π］

得x＝，

(4)由sinx＝0．1011，x∈［0，2π］

得x＝0．03π，1．97π或arcsin0．1011，π－arcsin0．1011．

(5)由tanx＝－4，x∈［0，2π］

得x＝0．58π，1．58π或π＋arctan(－4)，2π＋arctan(－4)

(6)由cosx＝1，x∈［0，2π］

得x＝0，2π

B组

1.解：由已知α是第四象限角

得2kπ＋＜α＜2kπ＋2π，(k∈Z)

(1)∴kπ＋＜＜kπ＋π∴的终边在第二或第四象限

(2)＋＜＜＋

即：90°＋k·120°＜＜30°＋90°＋k·120°

∴的终边在第二、第三或第四象限

(3)4kπ＋3π＜2α＜4kπ＋4π

即：2α的终边在第三或第四象限，也可在y轴的负半轴上.

2.解：由题意知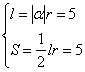

解之得｜α｜＝弧度

答：扇形中心角度数约为143°

3.解：cosα＋sinα＝cosα·

＝cosα·＝cosα(－(α为第二象限角)

4.解：由tanα＝－

(1)

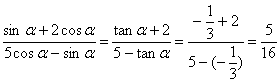
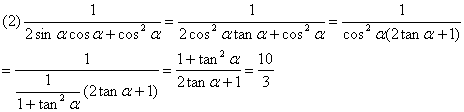
5.证明：左边＝

＝

＝

＝

＝sinα＋cosα＝右边

6.证明：∵xcosθ＝a，ycotθ＝b，(a≠0，ｂ≠0)

7.证明：(1)左边＝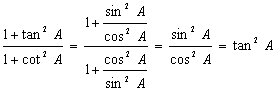

右边＝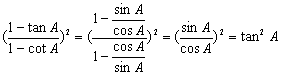

∴

(2)左边＝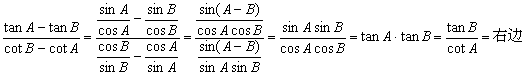

8.证明：由tanθ＋sinθ＝a，tanθ－sinθ＝ｂ

得(ａ2－ｂ2)2＝(ａ－ｂ)2(ａ＋ｂ)2＝(2sinθ)2(2tanθ)2＝16sin2θ·tan2θ

16ab＝16(tanθ＋sinθ)(tanθ－sinθ)＝16(tan2θ－sin2θ)

＝16sin2θ(－1)＝16sin2θ＝16sin2θtan2θ

∴(ａ2－ｂ2)2＝16ａｂ

9.证明：由3sinβ＝sin(2α＋β)

得3sin［(α＋β)－α］＝sin［(α＋β)＋α］

＝3sin(α＋β)cosα－3cos(α＋β)sinα

＝sin(α＋β)cosα＋cos(α＋β)sinα

∴2sin(α＋β)cosα=4cos(α＋β)sinα

∴tan(α＋β)＝2tanα

评述：等式两边主要是角的差异，应从变换条件中的角入手.

10.解：由已知cos(＋x)＝，＜x＜

得：cos2(＋x)＝2cos2(＋x)－1＝cos(＋2x)＝－sin2x＝－

∴sin2x＝，sin(＋x)＝－

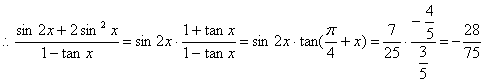
11．解：(1)当2kπ≤2x－≤2kπ＋π，(k∈Z)

即kπ＋≤x≤kπ＋时

y＝3cos(2x－)是减函数

(2)当2kπ＋≤－3x＋≤2kπ＋，(k∈Z)

即－＋≤x≤＋时

y＝sin(－3x＋)是减函数

12.解：由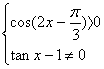

得－＋kπ＜x＜＋kπ或＋kπ＜x＜＋kπ(k∈Z)

∴函数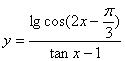的定义域为：

(－＋kπ，＋kπ)∪(＋kπ，＋kπ)，k∈Z

13.解：y＝sin2x＋2sinxcosx＋3cos2x(x∈R)

＝1＋sin2x＋2cos2x＝2＋sin2x＋cos2x

＝2＋sin(2x＋)

(1)周期T＝＝π

(2)当2kπ－≤2x＋≤2kπ＋，k∈Z

即－＋kπ≤x≤＋kπ时，原函数为增函数

∴函数在［－＋kπ，＋kπ］上是增函数

(3)图象可以由函数y＝sin2x，x∈R的图象向左平行移动个单位长度，再向上平行移动2个单位长度而得到

14.证明：由sinβ＝ｍsin(2α＋β)

得sin［(α＋β)－α］=ｍ·sin［(α＋β)＋α］

即sin(α＋β)cosα－cos(α＋β)sinα

＝ｍ［sin(α＋β)cosα＋cos(α＋β)sinα］

＝(1－ｍ)·sin(α＋β)cosα

＝(1＋ｍ)·cos(α＋β)sinα

∵ｍ≠1，α≠，α＋β≠＋kπ(k∈Z)

∴tan(α＋β)＝tanα

评述：此方法是综合法，利用综合法证明恒等式时，必须有分析的基础，此证法是观察到结论中的角构造：β＝(α＋β)－α；2α＋β＝(α＋β)＋α，证明时有的放矢，顺利完成证明.