椭圆的一些有趣性质及其应用 人教选修
教材中只介绍了椭圆的一些基本性质．在实际中，椭圆还有一些有趣的性质．探讨这些性质，不仅可以丰富解题思路，而且还可以培养我们的创新意识，在学习过程中会有所发现．本文介绍几个性质以示抛砖引玉．
一、椭圆上点对两焦点张直角的性质
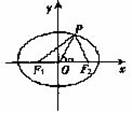
Ｐ是椭圆
上的一点，Ｆ１、Ｆ２是左、右焦点，Ｏ是椭圆中心，e是离心率，ＯＰ的倾斜角为α，则∠Ｆ１ＰＦ２＝９０°的充要条件是
．
证明 如图，在△Ｆ１ＰＦ２中，∠Ｆ１ＰＦ２为直角的充要条件是
（平面几何定理）
∵
设Ｐ点坐标为（x,y），则
，代入椭圆方程得：
∴整理得
即
∴
．
例１Ｐ是椭圆
上的一点，Ｆ１、Ｆ２为两焦点，若∠Ｆ１ＰＦ２＝９０°，试求
△ＰＦ１Ｆ２的面积．
解 设ＯＰ的倾斜角为α，又知
，代入可得
．
∴
二、椭圆准线上点对长轴顶点视角的性质
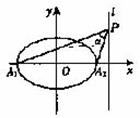椭圆
准线上的点对其长轴两顶点的视角为α，若椭圆的离心率为e，则α是锐角且
≤e．
证明 如图，设Ｐ在x轴上方，坐标为
∵
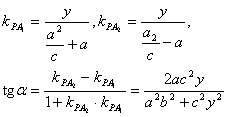
为锐角．
整理为y的方程
∵此方程有实根，∴
∴
∵α为锐角，∴
．
例２Ｐ是椭圆
右准线上的一点，点Ｐ对此椭圆左右两顶点Ａ１、Ａ２的视角为α，求α的最大值．
解 ∵
由题设及性质得
又知α为锐角，∴α的最大值为
．
三、椭圆中心点张直角的性质
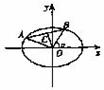若椭圆
上有两点Ａ、Ｂ，且ＯＡ⊥ＯＢ，则原点到弦ＡＢ的距离
．
证明 如图，设∠ＢＯＸ＝α，则∠ＡＯＸ＝
＋α，设ＯＢ＝m＞0,OA=n＞0,A点为
（－
，Ｂ点为（
），代入椭圆方程整理得
由等面积法得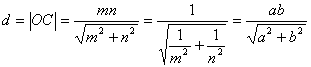
例３ 直线
与椭圆
交于Ａ、Ｂ两点，当k为何值时，以ＡＢ为直径的圆通过坐标原点．
解a＝２，
，∵ＡＢ为直径的圆过原点，∴ＯＡ⊥ＯＢ，由性质及原点到直线距离公式得
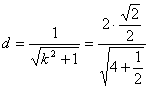,解之得
．
中考 高考名著
常用成语