椭圆中点弦的斜率公式及应用 人教选修
二次曲线的中点弦有许多有趣的性质，下面介绍椭圆中点弦的斜率公式，利用它可起到事半功倍的效果．
定理 设有二次曲线的方程为
Ａ、Ｂ两点在曲线上，Ｍ是弦ＡＢ的中点，Ｏ为坐标原点，则
．
证明 设Ａ、Ｂ两点坐标分别为（x1,y1）,(x2,y2)，则点Ｍ的坐标为（
）．
∵Ａ、Ｂ两点在曲线上，
∴
两式相减得：
整理得
，
又
，
．证毕．
注 特别地，当
＞０时，二次曲线为圆，显然ＯＭ⊥ＡＢ，有
．
例１ 过椭圆
内一点Ｄ（１，０）引动弦ＡＢ，求弦ＡＢ的中点Ｍ的轨迹方程．
解 设动点Ｍ的坐标为（x,y），则
由定理得
整理得
这就是点Ｍ的轨迹方程．
例２ 设椭圆
与直线
相交于Ａ、Ｂ两点，且
，又ＡＢ的中点Ｍ与原点Ｏ的连线的斜率为
，求a、b的值．
解 由定理得（－１）·
＝－
（１）
将
代入椭圆方程整理得：
设Ａ、Ｂ两点横坐标分别为x1、x2,则
∴
，∴
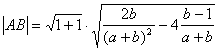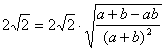
即
（２）
由（１）、（２）解得
中考 高考名著
常用成语